1. 概述
经常碰到类似这样的问题,要求找出文本 T[1..n]=abaabaabc 中模式 P[1..m]=abaabc 的出现/有效位移。汇总网上常用算法做一些记录。
2. 朴素算法
最简单直接的想法,就是对 n+m-1 个可能的每一个有效位移 s 检查是否满足条件 P[1..m]=T[s+1..s+m]。
func NaiveStringMatch(T,P string) []int {
result := make([]int, 0)
n, m := len(T), len(P)
for s:=0; s <= n-m; s++ {
if P[:m] == T[s:s+m] {
result = append(result, s)
}
}
return result
}
过程的运行时间为 O((n-m+1)m) 。这种匹配字符串匹配法的效率不高,其原因在于对于 s 的每个值,我们获得的关于文本的信息在考虑 s 的其它值时完全被忽略了。
3. The Knuth-Morris-Pratt 算法
在朴素算法的基础上,增加预处理过程,利用好每次匹配成功的部分所包含的信息,加快模式串滑动过程,无疑是加快匹配过程的有效方法。而 KMP 算法就是通过模式串本身的部分字符重复规律,实现快速匹配。
以模式串 P[1..m]=abaabc 为例,若匹配到如下情况:
abaabaabc
|||||
abaabc
按照朴素算法,则下一步将模式串右移一步重新匹配,KMP 算法则不然,直接右移3步:
abaabaabc
||
abaabc
3 由针对模式串的预处理过程得到。
讲预处理过程之前,先明确几个概念。从首字符至尾字符前的组合都可称之为字符串的前缀,同理,从任意非首字符开始至尾字符的组合都可称之为后缀。匹配成功的部分字符串的前缀和后缀的最大共有元素长度,可称之为部分匹配值,记为 π[1..m]。
预处理过程,即是计算部分匹配值的过程。示例部分匹配表(Partial Match Table)如下:
| i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P[i] | a | b | a | a | b | c |
| π[i] | 0 | 0 | 1 | 1 | 2 | 0 |
计算过程说明:
- π[1] = 0,a 仅一个字符,前缀和后缀为空集,共有元素最大长度为 0;
- π[2] = 0,ab 前缀为 a,后缀为 b,共有元素最大长度为 0;
- π[3] = 1,aba 前缀为 a、ab,后缀为 ba、a,共有元素最大长度为 1(a);
- π[4] = 1,abaa 前缀为 a、ab、aba,后缀为 baa、aa、a,共有元素最大长度为 1(a);
- π[5] = 2,abaab 前缀为 a、ab、aba、abaa,后缀为 baab、aab、ab、b,共有元素最大长度为 2(ab);
- π[6] = 0,abaabc 前缀为 a、ab、aba、abaa、abaab,后缀为 baabc、aabc、abc、bc、c,共有元素最大长度为 0;
而部分匹配成功后(匹配成功的前缀长度为 i)的右移步数为 i - π[i]。
综上,即为 KMP 算法的原理。
func GetPrefix(P string) []int {
m := len(P)
r := make([]int, m)
r[0] = 0
i, j := 1, 0
for i < m {
for j > 0 && P[j] != P[i] {
j = r[j-1]
}
if P[j] == P[i] {
j++
}
r[i] = j
i++
}
return r
}
func KMPMatch(T, P string) []int {
result := make([]int, 0)
n, m := len(T), len(P)
pi := GetPrefix(P)
i, j := 0, 0
for i + j < n {
if P[j] == T[i+j] {
j++
if j == m {
result = append(result, i)
i += j - pi[j-1]
j = pi[j-1]
}
} else if j > 0 {
i += j - pi[j-1]
j = 0
} else {
i++
}
}
return result
}
预处理过程耗时 O(m),匹配过程耗时 O(n)。
4. Boyer–Moore 算法
KMP 是一种前缀匹配算法,其效率也没有达到最高。很多编辑器都使用一种后缀匹配算法 BM 算法实现“查找”功能。经典的 BM 算法其实是对后缀朴素匹配算法的改进。
下面根据 Moore 教授的例子来解释这种算法。假定字符串为”HERE IS A SIMPLE EXAMPLE”,模式串为”EXAMPLE”,如下:
HERE IS A SIMPLE EXAMPLE
EXAMPLE
首先,字符串与模式串头部对齐,从尾部开始比较。‘S’ 与 ‘E’ 不匹配,我们称 ‘S’ 为一个坏字符(bad character)。由于 ‘S’ 并不包含在模式串中,因此可以直接将模式串滑动到 ‘S’ 的下一位。
HERE IS A SIMPLE EXAMPLE
EXAMPLE
‘P’ 也是一个坏字符,但是由于 ‘P’ 包含在模式串中,滑动模式串,使两个 ‘P’ 对齐。
HERE IS A SIMPLE EXAMPLE
EXAMPLE
由此总结出坏字符规则(如果坏字符不包含在模式串之中,则上一次出现位置可视为 -1):
后移位数 = 坏字符的位置 - 模式串中的上一次出现位置
依然从尾部开始比较。发现 “E”、“LE”、“PLE”、“MPLE” 都可以匹配成功,称之为好后缀(good suffix)。
此时 ‘I’ 为坏字符。若仍依据坏字符规则,需要将模式串向后移动 2 - (-1) = 3 位。但我们其实有更好的选择,也就是好后缀规则(好后缀位置以结束字符为准;如果好后缀仅出现一次,则上一次出现位置可视为 -1):
后移位数 = 好后缀的位置 - 模式串中的上一次出现位置
如果”好后缀”有多个,则除了最长的那个”好后缀”,其他”好后缀”的上一次出现位置必须在头部。比如,假定”BABCDAB”的”好后缀”是”DAB”、”AB”、”B”,请问这时”好后缀”的上一次出现位置是什么?回答是,此时采用的好后缀是”B”,它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个”好后缀”只出现一次,则可以把模式串改写成如下形式进行位置计算”(DA)BABCDAB”,即虚拟加入最前面的”DA”。
回到上文示例,所有的好后缀(MPLE、PLE、LE、E)之中,只有 ‘E’ 出现在模式串中并且还位于头部,所以后移 6 - 0 = 6 位。
事实上每次判断都可以依据两个规则得到两个位移值,BM 算法的基本思想就是移动二者中的较大值。
HERE IS A SIMPLE EXAMPLE
EXAMPLE
继续从尾部开始比较,‘P’ 是坏字符,依据坏字符规则,后移 6 - 4 = 2 位。
HERE IS A SIMPLE EXAMPLE
EXAMPLE
从尾部开始逐位比较,发现全部匹配。如果还要继续查找,则根据好后缀规则,后移 6 - 0 = 6 位,即头部的 ‘E’ 移到尾部的 ‘E’ 的位置。
func preBmBc(P string) []int {
r := make([]int, 256)
m := len(P)
for i := 0; i < 256; i++ {
r[i] = m
}
for i := 0; i < m-1; i++ {
r[P[i]] = m - i - 1
}
return r
}
func suffixes(P string) []int {
m := len(P)
suff := make([]int, m)
suff[m-1] = m
f, g := 0, m-1
for i := m - 2; i >= 0; i-- {
if i > g && suff[i+m-1-f] < i-g {
suff[i] = suff[i+m-1-f]
} else {
if i < g {
g = i
}
f = i
for g >= 0 && P[g] == P[g+m-1-f] {
g--
}
suff[i] = f - g
}
}
return suff
}
func preBmGs(P string) []int {
m := len(P)
suff := suffixes(P)
r := make([]int, m)
i, j := 0, 0
for i = 0; i < m; i++ {
r[i] = m
}
for i = m - 1; i >= 0; i-- {
if suff[i] == i+1 {
for ; j < m-1-i; j++ {
if r[j] == m {
r[j] = m - 1 - i
}
}
}
}
for i = 0; i <= m-2; i++ {
r[m-1-suff[i]] = m - 1 - i
}
return r
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
func BmMatch(T, P string) []int {
n, m := len(T), len(P)
bmGs := preBmGs(P)
bmBc := preBmBc(P)
result := make([]int, 0)
for j := 0; j <= n-m; {
i := m - 1
for i >= 0 && P[i] == T[i+j] {
i--
}
if i < 0 {
result = append(result, j)
j += bmGs[0]
} else {
j += max(bmGs[i], bmBc[T[i+j]]-m+1+i)
}
}
return result
}
预处理过程的时间复杂度是O(m+sigma),搜索过程O(mn)。最好情况下 BM 算法的时间复杂度为 O(n/m),最坏为 O(n)。
5. Boyer–Moore–Horspool 算法
Horspool 算法是 BM 算法的一种简化。在匹配到坏字符时,BM 算法依据坏字符规则将坏字符与模式串中上一次出现的位置对齐后再次匹配(或依据好后缀规则滑动模式串),而 Horspool 算法直接将当前匹配成功的最后一个字符与模式串中上一次出现的位置对齐后再次匹配。如下所示:
HERE IS A SIMPLE EXAMPLE HERE IS A SIMPLE EXAMPLE
|||| ---> |
EXAMPLE EXAMPLE
func HorspoolMatch(T, P string) []int {
n, m := len(T), len(P)
bmBc := preBmBc(P)
result := make([]int, 0)
for j := 0; j <= n-m; {
i := m - 1
if P[i] == T[i+j] && P[:i] == T[j:j+i] {
result = append(result, j)
}
j += bmBc[T[j+i]]
}
return result
}
算法的平均复杂度为 O(n), 最坏情况下为 O(nm)。
6. Sunday 算法
与 Horspool 算法类似, Sunday 算法也是对 BM 算法坏字符规则的改进。比 Horspool 算法关注当前匹配成功的最后一个字符更进一步,Sunday 算法直接观察当前匹配成功的最后一个字符的下一个字符。
func preSundayBc(P string) []int {
r := make([]int, 256)
m := len(P)
for i := 0; i < 256; i++ {
r[i] = m + 1
}
for i := 0; i < m; i++ {
r[P[i]] = m - i
}
return r
}
func SundayMatch(T, P string) []int {
n, m := len(T), len(P)
SundayBc := preSundayBc(P)
result := make([]int, 0)
for j := 0; j <= n-m; {
if P[:m] == T[j:j+m] {
result = append(result, j)
}
if j == n-m {
break
}
j += SundayBc[T[j+m]]
}
return result
}
算法在每次匹配都发现这个字符不在模式串中时达到最高效率 O(n/m),最坏为 O(nm)。
7. fastsearch 算法
是 python 中使用的字符串匹配算法,又被称为 BMHBNFS 算法,可以视作 BM、Horspool、Sunday 算法的综合:
func FSMatch(T, P string) []int {
n, m := len(T), len(P)
bmBc := preBmBc(P)
result := make([]int, 0)
for j := 0; j <= n-m; {
i := m - 1
if P[i] == T[i+j] { //boyer-moore
if P[:i] == T[j:j+i] {
result = append(result, j)
}
if j == n-m {
break
}
if bmBc[T[j+m]] == m {
j += m + 1 //sunday
} else {
j += bmBc[T[j+i]] //horspool
}
} else {
if j == n-m {
break
}
if bmBc[T[j+m]] == m {
j += m + 1 //sunday
} else {
j += 1
}
}
j += bmBc[T[j+i]]
}
return result
}
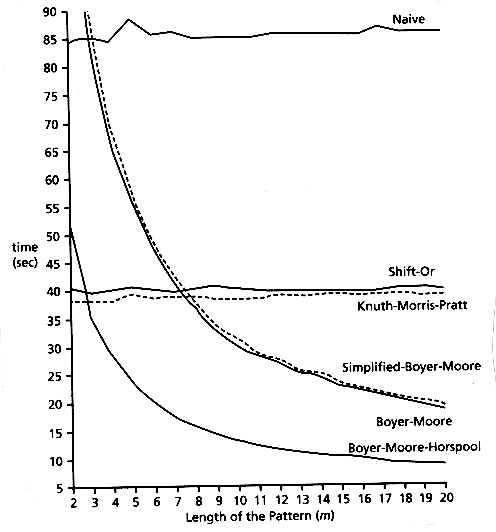
8. 小结
最后引用网上一个以自然语言测试的一些算法的效率比较图片,小字符集(如 DNA 匹配)结果可能不同: