1. 概述
回文子串也是字符串相关的常见题目。本文介绍一种时间复杂度为 O(n) 的最长回文子串算法。
2. 蛮力算法
先介绍一种简单思路。
给定长度为 n 的字符串,则其潜在的回文子串的中点有 2n-1 个位置,第1个字符处,第1、2个字符间、第2个字符处。。。第 n 个字符处。顺序考察每个中点,向左右做匹配扩展,记录当前最长的子串及其长度。
该算法的时间复杂度为 O(n^2),空间复杂度为 O(1)。简单实现如下:
func longestPalSubstr(str string) []string {
start, maxLength, length := 0, 0, len(str)
result := make([]string, 0)
if length == 0 {
return result
}
low, high := 0, 0
for center := 0; center < 2*length-1; center++ {
low = center / 2
high = low + center%2
for low >= 0 && high < length && str[low] == str[high] {
low--
high++
}
if high-low-1 > maxLength {
start = low + 1
maxLength = high - low - 1
result = make([]string, 1)
result[0] = str[start : start+maxLength]
} else if high-low-1 == maxLength {
start = low + 1
result = append(result, str[start:start+maxLength])
}
}
return result
}
3. 最长回文子串算法
考虑字符串“abababa”,它以中点 ‘b’ 对称,本身即是回文字符串。如果按照上述算法,对每个 2*n+1 个位置进行判断无疑会造成许多浪费。当在某一位置 P 计算完成后,尤其当出现一个长度为 L 的回文子串的时候,P+1 的位置已经不需要匹配其左右的每一个字符了。Manacher’s algorithm 正是利用这一特性降低复杂度。
继续探讨之前,我们先定义几个概念:
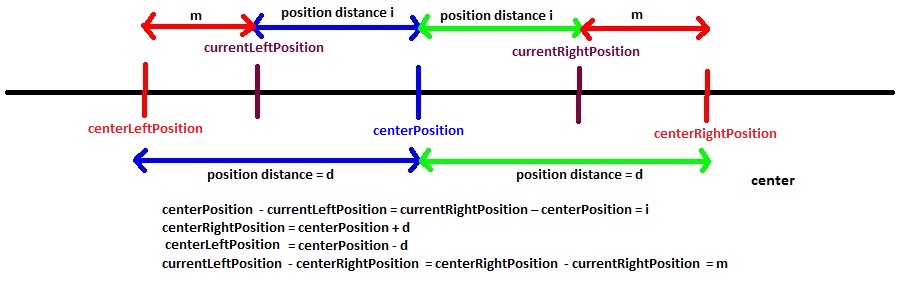
- centerPosition :是回文子串半径计算的基点位置,若以 centerPosition 为中点的 LPS 长度为 d,可记作
L[centerPosition] = d - centerRightPosition : 是 centerPosition 位置最长回文子串的右边界(字符)位置,
centerRightPosition = centerPosition + d - centerLeftPosition : 是 centerPosition 位置最长回文子串的左边界(字符)位置,
centerRightPosition = centerPosition - d - currentRightPosition :是逐字符考查 centerPosition 的最长回文子串过程中的临时右边界(字符)位置,逐字符增大
-
currentLeftPosition : 是逐字符考查 centerPosition 的最长回文子串过程中的临时左边界(字符)位置,逐字符减小
有如下关系及变形:
- centerPosition – currentLeftPosition = currentRightPosition – centerPosition
- currentLeftPosition = 2* centerPosition – currentRightPosition
- center palindrome : 以 centerPosition 位置为基点的最长回文子串
- i-left palindrome : 以 centerPosition-i 位置的为基点的最长回文子串
- i-right palindrome : 以 centerPosition+i 位置的为基点的最长回文子串
依据对称性,当一个较长的回文子串在其中点左半部分包含一个较短的回文子串时,其右半部分一定包含一个同样的回文子串。前提是这较短的回文子串不会越过较长的回文子串的边界。左半部分的回文子串不是长回文子串的前缀,或长回文子串已经是整个待考察字符串的后缀,都属于这类情况。
以“abababa”为例,假定已经计算了位置7的 LPS 长度如下:
| String S | | | a | | | b | | | a | | | b | | | a | | | b | | | a | | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Position i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| LPS Length L | 0 | 1 | 0 | 3 | 0 | 5 | 0 | 7 | ? | ? | ? | ? | ? | ? | ? |
将位置7作为 centerPosition, 已经得到 d = 7,centerLeftPosition = 0,centerRightPosition = 14。
计算 currentRightPosition = 8 位置的 LPS 长度。因为 L[currentLeftPosition] = L[6] = 0 < centerRightPosition – currentRightPosition = 14 – 8 = 6,表明左半部分的回文子串不是长回文子串的前缀,所以可以直接得到 L[currentRightPosition] = L[centerLeftPosition] = L[6] = 0。位置10、12也是这种情况。
计算 currentRightPosition = 9 位置的 LPS 长度。因为 L[currentLeftPosition] = L[5] = 5 = centerRightPosition – currentRightPosition = 14 - 9,表明长回文子串已经是整个待考察字符串的后缀,所以可以直接得到 L[currentRightPosition] = L[centerLeftPosition] = L[5] = 5。位置11、13、14也是这种情况。
把上述两种情形概括如下:
- Case 1:当 L[currentLeftPosition] < centerRightPosition – currentRightPosition 时,i-left palindrome 完全包含在 center palindrome 中且不是 center palindrome 的前缀,L[currentRightPosition] = L[currentLeftPosition]
- Case 2:当 L[currentLeftPosition] = centerRightPosition – currentRightPosition 并且 centerRightPosition = 2*n 时,i-left palindrome 完全包含在 center palindrome 中且是 center palindrome 的前缀,而 center palindrome 是整个字符串的后缀,L[currentRightPosition] = L[currentLeftPosition]
按照上述思路继续分析:
- Case 3:当 L[currentLeftPosition] = centerRightPosition – currentRightPosition 并且 centerRightPosition < 2*n 时,i-left palindrome 完全包含在 center palindrome 中且是 center palindrome 的前缀,而 center palindrome 不是是整个字符串的后缀,此时 L[currentRightPosition] >= L[currentLeftPosition],i-right palindrome 可能在 i-left palindrome 的基础上扩展
- Case 4:当 L[currentLeftPosition] > centerRightPosition – currentRightPosition 时, i-left palindrome 不完全包含在 center palindrome 中,此时 L[currentRightPosition] > = centerRightPosition – currentRightPosition,是否扩展需要进一步考察
以“babcbabcbaccba”为例,
| String S | | | b | | | a | | | b | | | c | | | b | | | a | | | b | | | c | | | b | | | a | | | c | | | c | | | b | | | a | | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Position i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| LPS Length L | 0 | 1 | 0 | 3 | 0 | 1 | 0 | 7 | 0 | 1 | 0 | 9 | 0 | 1 | 0 | 5 | 0 | 1 | 0 | 1 | 0 | 1 | 2 | 1 | 0 | 1 | 0 | 1 | 0 |
以 centerPosition = 7 位置为基准, d = 7, centerLeftPosition = 0,centerRightPosition = 14 < 2*n = 28,计算 currentRightPosition = 11 位置的 LPS 长度。因为 L[currentLeftPosition] = L[3] = 3 = centerRightPosition – currentRightPosition = 14 - 11,表明 i-left palindrome 完全包含在 center palindrome 中且是该 center palindrome 的前缀。但是由于 center palindrome 不是整个字符串的后缀,则 i-right palindrome 长度至少与 i-left palindrome 相同,还有可能更长。这就是 Case 3 情景。
以 centerPosition = 11 位置为基准, d = 9, centerLeftPosition = 2,centerRightPosition = 20 < 2*n = 28,计算 currentRightPosition = 15 位置的 LPS 长度。因为 L[currentLeftPosition] = L[7] = 7 > centerRightPosition – currentRightPosition = 20 - 15 = 5,表明 i-left palindrome 并不完全包含在 center palindrome 中。此时 i-right palindrome 至少包含 i-left palindrome 在center palindrome 中的部分,长度为 5,是否更长需要继续考察。这就是 Case 4 情景。
以上四种情景讨论完,就只剩一个问题了——如何决定及变更 centerPosition 呢?在 Case 3/4 情景中,若 i-right palindrome 扩展越过了 centerRightPosition 位置,就将 currentRightPosition 作为新的 centerPosition。
简单实现如下:
func longestPalSubstr(str string) []string {
if len(str) == 0 {
return make([]string, 0)
}
result := make([]string, 1)
result[0] = str[0:1]
n := 2*len(str) + 1
LPS := make([]int, n)
LPS[0], LPS[1] = 0, 1
centerPosition, centerRightPosition := 1, 2
maxLPSLength := 1
for i := 2; i < n; i++ { //currentRightPosition
currentLeftPosition := 2*centerPosition - i
expand := false
if d := centerRightPosition - i; d > 0 {
if LPS[currentLeftPosition] < d {
LPS[i] = LPS[currentLeftPosition] //Case 1
} else if LPS[currentLeftPosition] == d && i == n-1 {
LPS[i] = LPS[currentLeftPosition] //Case 2
} else if LPS[currentLeftPosition] == d && i < n-1 {
LPS[i] = LPS[currentLeftPosition] //Case 3
expand = true
} else if LPS[currentLeftPosition] > d {
LPS[i] = d //Case 4
expand = true
}
} else {
LPS[i] = 0
expand = true
}
if expand {
for i+LPS[i] < n && i-LPS[i] > 0 {
if (i+LPS[i]+1)%2 == 0 || i+LPS[i] < n-2 && str[(i+LPS[i]+1)/2] == str[(i-LPS[i]-1)/2] {
LPS[i]++
} else {
break
}
}
}
if LPS[i] > maxLPSLength {
maxLPSLength = LPS[i]
result = make([]string, 1)
result[0] = str[(i-LPS[i]+1)/2 : (i+LPS[i]+1)/2]
} else if LPS[i] == maxLPSLength {
result = append(result, str[(i-LPS[i]+1)/2:(i+LPS[i]+1)/2])
}
if i+LPS[i] > centerRightPosition {
centerPosition = i
centerRightPosition = i + LPS[i]
}
}
return result
}
内部循环中,LPS 分情景讨论的部分可以在理解后进行简化:
LPS[i] = 0
if d > 0 {
LPS[i] = min(LPS[currentLeftPosition], d)
}